Eric Weeks - personal pages - misc Lissajous Figures How to make them & their physical meaning. See the bottom of the page for links to other simple algorithms like this one.

weeks@physics.emory.edu

This was created with the following command:

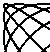
I don't know much about Lissajous figures; probably there's some place else on the web that you could learn a whole lot about them from. Basically they're sort of failed circles, or rather, a circle is the simplest Lissajous figure. By varying the rate at which X and Y change (changing the 18 and 20 above) you change how the Lissajous figure forms. Named after the French mathematician Jules-Antoine Lissajous.

Lissajous figures can be thought of as a simple physical system with springs. Suppose you have a weight hanging from a spring, and you pull the weight downward and let go. If you graph the vertical position -vs- time, you get a sine wave. (A real spring would also have friction, so the sine wave would get smaller as the spring lost energy.)

Imagine you have a weight hanging from a spring, with two horizontal springs attached to it, making an upside down T with the horizontal springs attached to walls. The weight can now move from side to side as well; if you pull it to one side, and let go, the weight will move in a sine wave again except with the horizontal position being what oscillates.

If you have both horizontal and vertical springs, and you move the weight diagonally (so that all of the springs are stretched) and let go, the position of the weight will trace out a Lissajous figure. The frequencies of the springs will determine how the Lissajous figure looks. For example, the figure at the top of the page might be from a weight/spring system with a vertical frequency of 1/20 and a horizontal frequency of 1/18.

You can get the same thing with a pendulum that has a different frequency for back-and-forth swinging and side-to-side swinging. The Natural Wonders stores (found in any mall!) sells a pendulum like this that makes Lissajous figures in sand.

On my old Apple //e the code looked something like this:

Click here if you'd like to see the source code for seq (actually, a perl script based on something I read in a book).

Click here for more information on psdraw.

Links...

• Odds and Ends: These are various tiny ideas that are simple to do which make interesting pictures, or are otherwise interesting (to me). Click one of the pictures below to see others.

• Eric's Home Page
• Other software
• Pictures I've made -- fractals, quasi crystals, cellular automata
• My research -- what I get paid for
• Graphics Techniques

• Questions? Comments? Send me email; email address below.

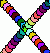
This page created August 22, 1996. Updated in 2004; thanks to Dan Valentine who emailed me to correct "Lissajou" to "Lissajous".