

Random close packing is the idea that particles often pack densely in jumbled random arrangements. This can be gumballs, beans, or rice in containers; sand at a beach; marbles in a bag. If all the particles are the same size, sometimes they pack less randomly: some of the gumballs in the image above are nestled into hexagonal structures (image credit: Eric).
IntroductionAs the list of papers above suggests, we've been interested in the question of how particles pack randomly for several years. This has been a mixture of experimental and computational work. A computational image is shown at right. The basic question we ask about random close packed structures is how densely they are packed: what is the volume fraction (phi) of the particles? That is, what fraction of the volume is solid particles, with the remainder being empty space between the particles? This is called by the Greek letter phi. For mixtures of spheres that are all the same size, the answer for the volume fraction of random close packing is known to be about 0.63 - 0.64. That is, just under two thirds of the volume is solid spheres. The exact number depends on how you do the experiment or simulation. Of course, one can ask more questions beyond just the volume fraction. What does it mean to pack particles "randomly"? What happens if the particles are different shapes, or mixtures of different sizes? In the picture above with gumballs, the container walls may be changing the packing and causing the hexagonal patterns some of the particles are making; how does a particle pack "randomly" against a wall? These are some of the questions we've investigated. |
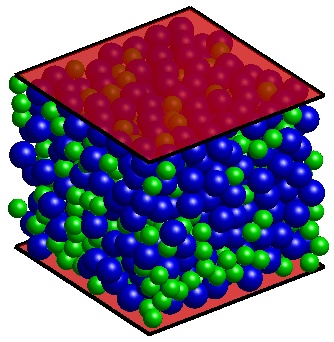
 A computer-generated random close packed configuration. The polydispersity (standard deviation of particle sizes divided by the mean size) is 0.4. |
|
|

|
|
|
|

|
|

|
|
We also tried some 2D experiments for a while; one experimental image is below. We used laser-cut plastic rings of various sizes in a large one meter diameter 2D container. Photo from Isabela Galoustian and David Meer.